svm (SVM path)

This file illustrates the notion of SVM path as a possible feature to improve selection of the cost parameter.

Documentation
Set rng
2D example (Linear SVM)
2D example (Non-linear SVM)
References

Documentation

The documentation for the svm class can be found here.

Set rng

Set random number generator seed:

rng(0)

2D example (Linear SVM)

On a simple example, obtain an initial DOE:

f=@(x)x(:,2)-sin(10*x(:,1))/4-0.5;
x=CODES.sampling.cvt(20,2);
y=f(x);

For different values of C, train an SVM and collect the values of b, beta and alpha for each value of C:

C=linspace(1,50,50)';
SVMs=cell(length(C),1);
bias=zeros(size(C,1),1);
betas=zeros(2,size(C,1));
alphas=zeros(size(x,1),size(C,1));
for i=1:length(C)
    SVMs{i}=CODES.fit.svm(x,y,'kernel','lin','C',C(i),'solver','primal');
    bias(i)=SVMs{i}.bias;
    betas(:,i)=SVMs{i}.beta;
    alphas(:,i)=SVMs{i}.alphas;
end

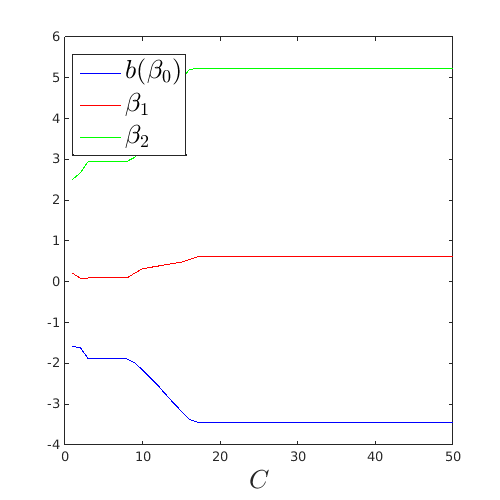
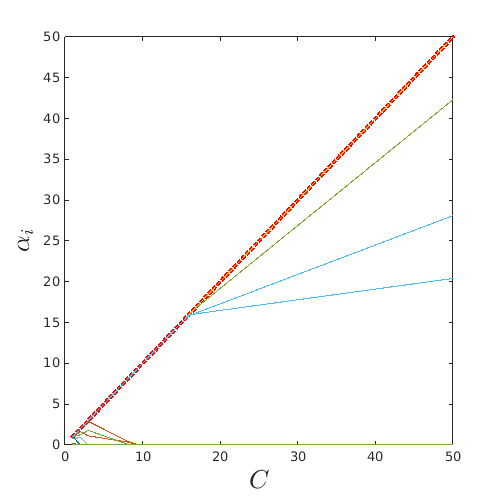
Plot the collected value. Observe the piecewise linear behavior:

figure('Position',[200 200 500 500])
plot(C,bias,'b')
hold on
plot(C,betas(1,:),'r')
plot(C,betas(2,:),'g')
leg=legend('$b (\beta_0)$','$\beta_1$','$\beta_2$');
set(leg,'interpreter','latex','FontSize',20,'Location','Best')
xlabel('$C$','interpreter','latex','FontSize',20)

figure('Position',[200 200 500 500])
plot(C,C,'r:','LineWidth',3)
hold on
plot(C,alphas)
xlabel('$C$','interpreter','latex','FontSize',20)
ylabel('$\alpha_i$','interpreter','latex','FontSize',20)

2D example (Non-linear SVM)

For different values of C (theta fixed), train an SVM and collect the values of b, beta and alpha for each value of C:

C=linspace(1,50,200)';
SVMs=cell(length(C),1);
bias=zeros(size(C,1),1);
betas=zeros(2,size(C,1));
alphas=zeros(size(x,1),size(C,1));
for i=1:length(C)
    SVMs{i}=CODES.fit.svm(x,y,'theta',0.7325,'kernel','gauss','C',C(i));
    bias(i)=SVMs{i}.bias;
    alphas(:,i)=SVMs{i}.alphas;
end

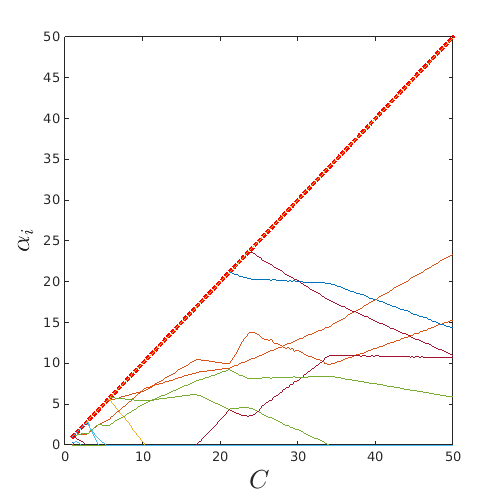
Plot the collected value. Observe the piecewise linear behavior (noise is due to numerical error in solver convergence):

figure('Position',[200 200 500 500])
plot(C,C,'r:','LineWidth',3)
hold on
plot(C,alphas)
xlabel('$C$','interpreter','latex','FontSize',20)
ylabel('$\alpha_i$','interpreter','latex','FontSize',20)

References

Hastie et al. (2004): Hastie T., Rosset S., Tibshirani R., and Zhu J. (2004)The entire regularization path for the support vector machine. Journal of Machine Learning Research, 5:1391-1415.