Examples / Reliability assessment / mc

This file is a complete demo of the capability of the mc function from the CODES toolbox.

Documentation
Set rng
Simple linear example
Sampler or Tinv
Save Monte-Carlo samples
Use user defined random sample
Compute sensitivities dPfdtheta
Compute sensitivities dPfdz

Documentation

The documentation for the mc function can be found here.

Set rng

Set random number generator seed:

rng(0)

Simple linear example

Compute the CMC 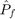$\hat{P}_f$ on a simple linear example:

g=@CODES.test.lin;
res_mc=CODES.reliability.mc(g,2,'vectorial',true);
disp(res_mc)

          Pf: 0.0014
        beta: 3.0000
    LS_count: 1000000
         CoV: 2.7198
       CI_Pf: [0.0013 0.0014]
     CI_beta: [2.9841 3.0166]

Ensure a CoV of variation of at most 1%:

res_mc=CODES.reliability.mc(g,2,'vectorial',true,'CoV',1);
disp(res_mc)

          Pf: 0.0013
        beta: 3.0041
    LS_count: 7506374
         CoV: 0.9995
       CI_Pf: [0.0013 0.0014]
     CI_beta: [2.9982 3.0102]

Sampler or Tinv

Sampler and Tinv are mutually exclusive and there almost always exist an equivalent from one to another. For example, for exponential distribution:

sampler=@(N)exprnd(0.5,N,2);
Tinv=@(u)expinv(normcdf(u),0.5);
res_mc1=CODES.reliability.mc(g,2,'vectorial',true,'CoV',1,'sampler',sampler);
res_mc2=CODES.reliability.mc(g,2,'vectorial',true,'CoV',1,'Tinv',Tinv);
CODES.common.disp_matrix([res_mc1.Pf res_mc2.Pf;res_mc1.beta res_mc2.beta;...
    res_mc1.CoV res_mc2.CoV],{'Pf','beta','CoV'},{'Sampler','Tinv'})

         Sampler        Tinv
  Pf  0.00194826  0.00197048
beta     2.88642     2.88285
 CoV    0.999675    0.999865

In thegeneral case, the sampler function can be slightly more involved. For example, if the joint PDF is defined by 2 independent gaussian with respective mean 5 and 3 and respective standard deviation 2 and 1, a sampler function should read:

sampler=@(N)normrnd(repmat([5 3],N,1),repmat([2 1],N,1));
res_mc1=CODES.reliability.mc(g,2,'vectorial',true,'CoV',1,'sampler',sampler);
disp(res_mc1)

          Pf: 0.9536
        beta: -1.6806
    LS_count: 1000000
         CoV: 0.0221
       CI_Pf: [0.9532 0.9540]
     CI_beta: [-1.6849 -1.6764]

Save Monte-Carlo samples

res_mc=CODES.reliability.mc(g,2,'vectorial',true,'store',true);
disp(res_mc)

          Pf: 0.0014
        beta: 2.9989
    LS_count: 1000000
         CoV: 2.7148
       CI_Pf: [0.0013 0.0014]
     CI_beta: [2.9830 3.0155]
           X: [1000000x2 double]
           Y: [1000000x1 double]

Use user defined random sample

res_mc=CODES.reliability.mc(g,normrnd(0,1,1e5,2),'vectorial',true);
disp(res_mc)

          Pf: 0.0011
        beta: 3.0673
    LS_count: 100000
         CoV: 9.6173
       CI_Pf: [8.7642e-04 0.0013]
     CI_beta: [3.0153 3.1292]

Compute sensitivities dPfdtheta

Here are two examples on how to compute sensitivities of the estimated probability of failure. See mc help for details on the options.

Using a simple standard gaussian space and a linear limit state:

d=3;
g=@(x)-x(:,2)-x(:,1)+d;
beta=@(mus)(d-sum(mus))/sqrt(2);
dbetadtheta=-1/sqrt(2)*ones(1,2);
dPdfdtheta=@(mus)-dbetadtheta*normpdf(-beta(mus));

lnPDF=@(x,mus)sum(log(normpdf(x,mus,[1 1])),2);
dlnPDF=@(x,mus)bsxfun(@minus,x,repmat(mus,size(x,1),1));

tic;
res_mc=CODES.reliability.mc(g,2,'vectorial',true,'lnPDF',lnPDF,'theta',[0 0]);
time_ln=toc;
tic;
res_mc1=CODES.reliability.mc(g,2,'vectorial',true,'dlnPDF',@(x)dlnPDF(x,[0 0]));
time_dln=toc;

CODES.common.disp_matrix([res_mc.dPfdtheta res_mc.dbetadtheta time_ln;...
    res_mc1.dPfdtheta res_mc1.dbetadtheta time_dln;
    dPdfdtheta([0 0]) dbetadtheta 0],{'ln','dln','ref'},...
    {'dPfdtheta1','dPfdtheta2','dbetadtheta1','dbetadtheta2','time'});

     dPfdtheta1  dPfdtheta2  dbetadtheta1  dbetadtheta2      time
 ln   0.0294346   0.0297914     -0.701841     -0.710351   23.0342
dln   0.0296074   0.0294111      -0.70858     -0.703883  0.091404
ref   0.0297326   0.0297326     -0.707107     -0.707107         0

Compute sensitivities dPfdz