CODES / common / grad_fd
Gradient of f at x using finite difference
Contents
Syntax
- grad=CODES.common.grad_fd(f,x) compute the finite differences of f at x.
- [grad,fx]=CODES.common.grad_fd(...) returns the function values f(x).
- [...]=CODES.common.grad_fd(...,param,value) uses a list of parameters param and values value (c.f., parameter table).
Usage
If f returns only one output, grad is a size(x) matrix. If f returns multiple outputs, f must return a nY row vector and grad is the Jacobian (nY x size(x,2) x size(x,1)) three dimensional matrix.
Parameters
| param | value | Description |
|---|---|---|
| 'rel_diff' | positive numeric, {1e-5} | Finite difference step size. |
| 'type' | 'forward', 'backward' or {'central'} | Type of finite difference. |
| 'fx' | numeric, { [ ] } | Function value at x f(x) (save one function evaluation). |
| 'vectorial' | logical {false} | Wether f is vectorial or not. |
Example
Compute finite diffence for:
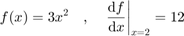
f=@(x)3*x.^2; grad_c=CODES.common.grad_fd(f,2,'rel_diff',1e-3); grad_f=CODES.common.grad_fd(f,2,'type','forward','rel_diff',1e-3); grad_b=CODES.common.grad_fd(f,2,'type','backward','rel_diff',1e-3); CODES.common.disp_matrix([grad_c grad_f grad_b],[],... {'Central','Forward','Backward'})
Central Forward Backward
12 12.003 11.997
See also
Copyright © 2015 Computational Optimal Design of Engineering Systems (CODES) Laboratory. University of Arizona.

|
Computational Optimal Design of Engineering Systems |

|