mcmc

Component Metropolis-Hastings

Syntax
Description
Parameters
Example
References

Syntax

x=CODEScommon.mcmc(sites,N,PDFs_target) performs component Metropolis-Hastings. sites is a (nc x dim) matrix used to start nc Markov-chain. Each chain as N samples and x is the (N x dim x Nc) matrix of generated samples. PDFs_target is the target marginal PDFs. For a (n x dim) sample, PDFs_target(x) should return a (n x dim) matrix of marginal PDF values.
[x,y]=CODEScommon.mcmc(sites,N,PDFs_target) returns the (N x 1 x nc) array y of rejection function values (requires a rejection function).
[x,y,dy]=CODEScommon.mcmc(sites,N,PDFs_target) returns the (N x dim x Nc) array dy of rejection gradient (requires a rejection function and gradient option).
[...]=CODEScommon.mcmc(...,param,value) uses a list of parameters param and values value (see, parameter table)

Description

Component Metropolis-Hasting as discussed in Au & Beck (2001). As opposed to the regular algorithm where a joint target and proposal PDF is provided, this variant works with marginal target and proposal PDFs. Acceptance/rejection decision is made dimension per dimension.

Parameters

param value Description

'prop_rand' function_handle, {@(x)normrnd(x,ones(size(x)))} Proposal random sampler. For a (n x dim) sample x, returns a (n x dim) sample of proposed candidates. By default, uses normal with mean x and standard deviation 1.

'burnin' positive integer, {0} Number of samples to be “burned” at the begining.

'rejection' function_handle, {-1} A rejection function. For a (n x dim) sample x, rejection(x) should return a (n x 1) array of rejection function value. Samples are rejected if rejection function value is positive.

'gradient' logical, {false} Wether or not gradient of the rejection function should be returned. If 'on', rejection should return 2 outputs [y,dy] where y and dy are the (n x 1) array of rejection function values and the (n x dim) array of rejection gradient respectively.

'initial_values' numeric, { [ ] } An array of initial rejection values.

'initial_gradients' numeric, { [ ] } An array of initial gradients.

`param`	`value`	Description
'prop_rand'	`function_handle`, {`@(x)normrnd(x,ones(size(x)))`}	Proposal random sampler. For a `(n x dim)` sample `x`, returns a `(n x dim)` sample of proposed candidates. By default, uses normal with mean `x` and standard deviation 1.
'burnin'	positive integer, {0}	Number of samples to be “burned” at the begining.
'rejection'	`function_handle`, {`-1`}	A rejection function. For a `(n x dim)` sample `x`, `rejection(x)` should return a `(n x 1)` array of rejection function value. Samples are rejected if rejection function value is positive.
'gradient'	logical, {`false`}	Wether or not gradient of the rejection function should be returned. If 'on', `rejection` should return 2 outputs `[y,dy]` where `y` and `dy` are the `(n x 1)` array of rejection function values and the `(n x dim)` array of rejection gradient respectively.
'initial_values'	numeric, { [ ] }	An array of initial rejection values.
'initial_gradients'	numeric, { [ ] }	An array of initial gradients.

Example

Generate samples from an exponential distribution (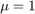 $\mu=1$ ) while rejecting samples such that:

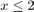
$x\leq 2$

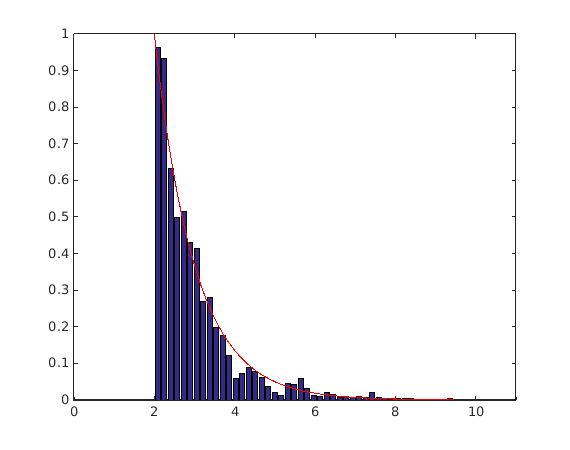
pdf=@(x)exppdf(x,1);
rejection=@(x)2-x;
x_mcmc=CODES.common.mcmc(3,2000,pdf,'rejection',rejection);
CODES.common.hist_fd(x_mcmc,@(x)exppdf(x,1)/(1-expcdf(2,1)))
axis([0 11 0 1])

References

Au & Beck (2001): Au, S.-K., & Beck, J. L. (2001). Estimation of small failure probabilities in high dimensions by subset simulation. Probabilistic Engineering Mechanics, 16(4), 263-277. DOI