meta

_A general meta-modeling class which contains a wide array of options

Syntax
Scaling
Parameters
Properties
Methods

Syntax

meta=CODES.sampling.meta(x,y) builds a meta-model based on training set (x,y).
meta=CODES.sampling.meta(...,param,value) uses a list of parameters param and values value (c.f., parameter table)

Scaling

Scaling input data is always good practice. For example, a training set with n samples of dimension m is defined as:

$\mathbf{X}=\left[\begin{array}{ccc}x_1^{(1)}&\ldots&x_m^{(1)}\\\vdots&\ddots&\vdots\\x_1^{(n)}&\ldots&x_m^{(n)}\end{array}\right]$

Two main scaling are proposed:

"Square" scaling

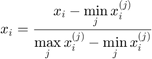
$x_i=\frac{x_i-\mathop{\min}\limits_{j}x_i^{(j)}}{\mathop{\max}\limits_{j}x_i^{(j)}-\mathop{\min}\limits_{j}x_i^{(j)}}$

"Circle" scaling

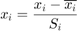
$x_i=\frac{x_i-\overline{x_i}}{S_i}$

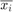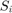where $\overline{x_i}$ and $S_i$ are respectively sample mean and standard deviation such that:

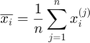
$\overline{x_i}=\frac{1}{n}\sum_{j=1}^nx_i^{(j)}$

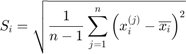
$S_i=\sqrt{\frac{1}{n-1}\sum_{j=1}^n\left(x_i^{(j)}-\overline{x_i}\right)^2}$

Parameters

param value Description

'scale' {'square'}, 'circle', 'none' Define scaling method for the inputs (c.f., Scaling for details)

'UseParallel' logical, {false} Switch to use parallel settings

param	value	Description
'scale'	{'square'}, 'circle', 'none'	Define scaling method for the inputs (c.f., Scaling for details)
'UseParallel'	logical, {`false`}	Switch to use parallel settings

Properties

X: Unscaled training samples
Y: Training values
labels: Training labels (used for classification only)
X_sc: Scaled training samples
dim: Training samples dimension
n: number of training samples
scalers: Scaling factor to account for in gradient calculations

Methods

Methods available for the class meta are described here

Computational Optimal Design of
Engineering Systems