corr

Compute correlation coefficient

Syntax
Description
Sampling distribution
Parameters
Example
Mini Tutorial
References

Syntax

res=CODES.sensitivity.corr(X,Y) computes selected correlation coefficient rho (or tau) between X and Y.
res=CODES.sensitivity.corr(...,param,value) uses a list of parameters param and values value (c.f., parameter table).

Description

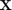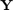Compute standard coefficient between $\mathbf{X}$ and $\mathbf{Y}$ . Essentially uses matlab built in corr but adds confidence interval (estimates and bootstrap) and some plotting capability.

Sampling distribution

Approximation of the confidence interval are obtained through (approximated) sampling distribution of the correlation coefficient.

Pearson, using the Fisher transform:

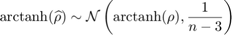
$\mbox{arctanh}(\widehat{\rho})\sim\mathcal{N}\left(\mbox{arctanh}(\rho),\frac{1}{n-3}\right)$

Spearman, using the Fisher transform (only exact for $\rho=0$ ):

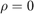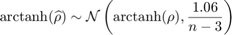
$\mbox{arctanh}(\widehat{\rho})\sim\mathcal{N}\left(\mbox{arctanh}(\rho),\frac{1.06}{n-3}\right)$

Kendall, using normal assumption (only exact for 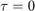$\tau=0$ , bootstrap should be preferred here):

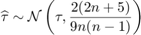
$\widehat{\tau}\sim\mathcal{N}\left(\tau,\frac{2(2n+5)}{9n(n-1)}\right)$

where $n$ is the number of realizations used in the estimates.

Parameters

param value Description

'type' {'pearson'}, 'spearman', 'kendall' Correlation coefficient type. 'type' can also be a cell array to return several coefficients at once.

'alpha' positive integer, {0.05} Significance level for confidence interval.

'CI' logical, {false} Whether to return approximations of confidence interval, see Sampling distribution.

'CI_boot' logical, {false} Whether to return bootstrapped confidence interval.

'nb_boot' numeric, {200} Number of bootstraps

'boot_type' {'bca'}, 'norm', 'per', 'cper' Type of bootstrap confidence interval (Efron, 1987)

'pie_plot' logical, {false} Whether to provide a pie plot of the output.

'err_plot' logical, {false} Whether to provide an error plot of the output.

'xlabel' cell, { [ ] } Variable labels to be used in plots.

`param`	`value`	Description
'type'	{'pearson'}, 'spearman', 'kendall'	Correlation coefficient type. 'type' can also be a cell array to return several coefficients at once.
'alpha'	positive integer, {0.05}	Significance level for confidence interval.
'CI'	logical, {`false`}	Whether to return approximations of confidence interval, see Sampling distribution.
'CI_boot'	logical, {`false`}	Whether to return bootstrapped confidence interval.
'nb_boot'	numeric, {200}	Number of bootstraps
'boot_type'	{'bca'}, 'norm', 'per', 'cper'	Type of bootstrap confidence interval (Efron, 1987)
'pie_plot'	logical, {`false`}	Whether to provide a pie plot of the output.
'err_plot'	logical, {`false`}	Whether to provide an error plot of the output.
'xlabel'	cell, { [ ] }	Variable labels to be used in plots.

Example

Compute and plot an anti-locking sample

f=@(x)1/8*prod(3*x.^2+1,2);
X=rand(100,3);Y=f(X);
res=CODES.sensitivity.corr(X,Y);
disp(res.pearson)

            rho: [1x3 double]
     pie_plot(): pie plot of the coefficients

Mini Tutorial

A cmini tutorial of the capabilities of the corr function.

References

Efron (1987): Efron, B. (1987). Better bootstrap confidence intervals. Journal of the American Statistical Association, 82(397), 171-185. DOI

Computational Optimal Design of
Engineering Systems