CODES / sensitivity / dgsm
Compute derivative-based sensitivity measure
Contents
Syntax
- res=CODES.sensitivity.dgsm(dY) computes sensitivity measure based on the (n x dim) matrix of partial derivatives (or gradients) at n realizations.
- res=CODES.sensitivity.dgsm(...,param,value) uses a list of parameters param and values value (c.f., parameter table)
Description
Compute derivative-based sensitivity measure of three types:
- Elementary effects (EE) (Morris, 1991):
![$$\mu_i^0=\mathbf{E}\left[\frac{\partial f}{\partial x_i}\right]\qquad \sigma_i^0=\mathbf{V}\left[\frac{\partial f}{\partial x_i}\right]$$](dgsm_eq17483243123900326846.png)
- DGSM1 (Campolongo et al., 2007):
![$$\mu_i^1=\mathbf{E}\left[\left|\frac{\partial f}{\partial x_i}\right|\right]\qquad \sigma_i^1=\mathbf{V}\left[\left|\frac{\partial f}{\partial x_i}\right|\right]$$](dgsm_eq03923934782196597382.png)
- DGSM2 (Sobol' & Kucherenko, 2009):
![$$\mu_i^0=\mathbf{E}\left[\frac{\partial f}{\partial x_i}^2\right]\qquad \sigma_i^0=\mathbf{V}\left[\frac{\partial f}{\partial x_i}^2\right]$$](dgsm_eq08889669574390529152.png)
Sampling distribution
Approximations of the confidence interval are obtained based on sampling distributions of sampling mean and standard deviation:
- Sample mean, relatively accurate for all distributions due to CLT (Rice, 2006):
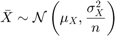
- Sample standard deviation, only accurate for normal distributions:
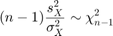
Bootstrapped CI would be more appropriate here.
Parameters
| param | value | Description |
|---|---|---|
| 'type' | {'EE'}, 'DGSM1', 'DGSM2' | Derivative-based measure type. 'type' can also be a cell array to return several measures at once. |
| 'alpha' | positive integer, {0.05} | Significance level for confidence interval. |
| 'CI' | logical, {false} | Whether to return approximations of confidence interval, see Sampling distribution. |
| 'CI_boot' | logical, {false} | Whether to return bootstraped confidence interval. |
| 'nb_boot' | numeric, {200} | Number of bootstraps |
| 'boot_type' | {'bca'}, 'norm', 'per', 'cper' | Type of bootstrap confidence interval (Efron, 1987) |
| 'pie_plot' | logical, {false} | Whether to provide a pie plot of the output |
| 'err_plot' | logical, {false} | Whether to provide an error plot of the output |
| 'xlabel' | cell, { [ ] } | Variable labels to be used in plots |
Example
Compute and plot an anti-locking sample
f=@(x)1/8*prod(3*x.^2+1,2); X=rand(100,3);dY=CODES.common.grad_fd(f,X); res=CODES.sensitivity.dgsm(dY); disp(res.EE)
mu: [1x3 double]
std: [1x3 double]
pie_plot(): pie plot of the differential coefficients
Mini Tutorial
 |
A mini tutorial of the capabilities of the corr function. |
References
- Efron (1987): Efron, B. (1987). Better bootstrap confidence intervals. Journal of the American Statistical Association, 82(397), 171-185. DOI
- Morris (1991): Morris, M. D. (1991). Factorial sampling plans for preliminary computational experiments. Technometrics, 33(2), 161-174.
- Campolongo et al. (2007): Campolongo, F., Cariboni, J., & Saltelli, A. (2007). An effective screening design for sensitivity analysis of large models. Environmental Modelling & Software, 22(10), 1509-1518.
- Sobol' & Kucherenko (2009): Sobol', I. M., & Kucherenko, S. (2009). Derivative based global sensitivity measures and their links with global sensitivity indices. Mathematics and Computers in Simulation, 79(10), 3009-3017.
- Rice (2006): Rice, J. (2006). Mathematical Statistics and Data Analysis. Cengage Learning.
Copyright © 2015 Computational Optimal Design of Engineering Systems (CODES) Laboratory. University of Arizona.

|
Computational Optimal Design of Engineering Systems |

|