form

First Order Reliability Method

Syntax
Description
Solvers
Parameters
Example
Mini Tutorial
References
See also

Syntax

res=CODES.reliability.form(g,dim) computes a FORM estimate of the probability that 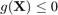$g(\mathbf{X})\leq 0$ . The dim random variables 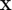$\mathbf{X}$ are independent standard gaussian.
res=CODES.reliability.form(...,param,value) uses a list of parameters param and values value (see, parameter table).

Description

For a given limit state function 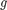$g$ and a joint PDF 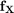$\mathbf{f}_\mathbf{X}$ , the probability of failure is:

$P_f=\int_\Omega I[g(\mathbf{x})\leq 0]\mathbf{f}_\mathbf{X}(\mathbf{x})\mathrm d\mathbf{x}$

An approximation of 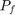$P_f$ is given by the First Order Reliability Method (FORM) which assumes that the limit state function is linear in the standard normal space. It is based on the notion of most probable point (MPP) 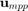$\mathbf{u}_{mpp}$ which is found by solving the following optimization problem (RIA approach):

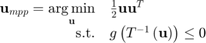
$\begin{array}{rl}\mathbf{u}_{mpp}=\mathop{\arg\min}\limits_{\mathbf{u}}&\frac{1}{2}\mathbf{u}\mathbf{u}^T\\\mbox{s.t.} & g\left(T^{-1}\left(\mathbf{u}\right)\right)\leq 0\end{array}$

The reliability index 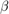$\beta$ is defined as the algebraic distance from the origin to the MPP in the standard normal space. The probability of failure is then approximated as:

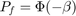
$P_f=\Phi(-\beta)$

Sensitivities of 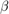$\beta$ with respect to distribution hyper-parameters 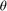$\theta$ and deterministic variables $\mathbf{z}$ are defined as:

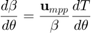
$\displaystyle\frac{d\beta}{d\theta}=\frac{\mathbf{u}_{mpp}}{\beta}\frac{dT}{d\theta}$

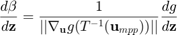
$\displaystyle\frac{d\beta}{d\mathbf{z}}=\frac{1}{||\nabla_\mathbf{u}g(T^{-1}(\mathbf{u}_{mpp}))||}\frac{dg}{d\mathbf{z}}$

Solvers

Currently available solvers:

'sqp', matlab fmincon using sqp algorithm
'hl-rf', Hasofer & Lind (1974) and Rackwitz & Fiessler (1978)
'ihl-rf', Liu & Der Kiureghian (1991)
'jhl-rf', Zhang & Der Kiureghian (1995)

Parameters

param value Description

'solver' {'sqp'}, 'hl-rf', 'ihl-rf', 'jhl-rf' Defines which RIA solver to use, see Solvers.

'Tinv' function_handle, { [ ] } An inverse transformation function that transform realizations from a standard gaussian space into the desired space. For example, for an exponential space Tinv=@(u)expinv(normcdf(u),1).

'LS_grad' logical, {false} Whether the limit state function g also return gradients with respect to x.

'rel_diff' positive, {1e-5} Perturbation used for finite difference.

'eps' positive, {1e-4} Convergence tolerance.

'iter_max' positive integer, {100} Maximum number of iterations.

'vectorial' logical, {false} Whether the limit state function g is vectorial.

'display' {'none'}, 'final', 'iter' Defines the verbose level.

'gz' function_handle g as a function of x and z, used for dPf/dz (see Mini Tutorial for an example).

'dgdz' function_handle dg/dz as a function of x and z, used for dPf/dz (see Mini Tutorial for an example).

'z' real value z value, used for dPf/dz (see Mini Tutorial for an example).

'T' function_handle Transformation T (inverse of Tinv) as a function of x and theta, used for dPf/dtheta (see Mini Tutorial for an example).

'dTdtheta' function_handle dT/dtheta as a function of x and theta, used for dPf/dtheta (see Mini Tutorial for an example).

'theta' real value theta value, used for dPf/dtheta (see Mini Tutorial for an example).

`param`	`value`	Description
'solver'	{'sqp'}, 'hl-rf', 'ihl-rf', 'jhl-rf'	Defines which RIA solver to use, see Solvers.
'Tinv'	`function_handle`, { [ ] }	An inverse transformation function that transform realizations from a standard gaussian space into the desired space. For example, for an exponential space `Tinv=@(u)expinv(normcdf(u),1)`.
'LS_grad'	logical, {`false`}	Whether the limit state function `g` also return gradients with respect to x.
'rel_diff'	positive, {1e-5}	Perturbation used for finite difference.
'eps'	positive, {1e-4}	Convergence tolerance.
'iter_max'	positive integer, {100}	Maximum number of iterations.
'vectorial'	logical, {`false`}	Whether the limit state function `g` is vectorial.
'display'	{'none'}, 'final', 'iter'	Defines the verbose level.
'gz'	`function_handle`	g as a function of x and z, used for dPf/dz (see Mini Tutorial for an example).
'dgdz'	`function_handle`	dg/dz as a function of x and z, used for dPf/dz (see Mini Tutorial for an example).
'z'	real value	z value, used for dPf/dz (see Mini Tutorial for an example).
'T'	`function_handle`	Transformation T (inverse of Tinv) as a function of x and theta, used for dPf/dtheta (see Mini Tutorial for an example).
'dTdtheta'	`function_handle`	dT/dtheta as a function of x and theta, used for dPf/dtheta (see Mini Tutorial for an example).
'theta'	real value	theta value, used for dPf/dtheta (see Mini Tutorial for an example).

Example

Compute and plot a generalized "max-min" sample

g=@CODES.test.lin;
res=CODES.reliability.form(g,2);
disp(res)

          Pf: 0.0013
        beta: 3.0000
       alpha: [0.7071 0.7071]
    LS_count: 6
         MPP: [2.1213 2.1213]
        uMPP: [2.1213 2.1213]

Mini Tutorial

A mini tutorial of the capabilities of the form function.

References

Hasofer & Lind (1974): Hasofer, A. M., & Lind, N. C. (1974). An exact and invariant first-order reliability format. Journal of Engineering Mechanics, 100(1), 111-121.
Rackwitz & Fiessler (1978): Rackwitz, R. & Fiessler, B. (1978). Structural reliability under combined random load sequences. Computers & Structures, 9(5), 489-494. DOI
Liu & Der Kiureghian (1991): Liu, P.-L., & Der Kiureghian, A. (1991). Optimization algorithms for structural reliability. Structural Safety, 9(3), 161-177. DOI
Zhang & Der Kiureghian (1995): Zhang, Y., & Der Kiureghian, A. (1995). Two Improved Algorithms for Reliability Analysis. In Proceedings of the sixth IFIP WG7.5 working conference on reliability and optimization of structural systems (pp. 297-304). DOI