sorm

Second-order reliability method

Syntax
Approximations
Parameters
Example
Mini Tutorial
References
See also

Syntax

res=CODES.reliability.sorm(g,dim) compute a SORM estimate of the probability that 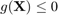$g(\mathbf{X})\leq 0$ . The dim random variables 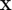$\mathbf{X}$ are independent standard gaussian.
res=CODES.reliability.sorm(...,param,value) uses a list of parameters param and values value (see, parameter table)

Approximations

For a given limit state function 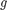$g$ and a joint PDF 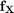$\mathbf{f}_\mathbf{X}$ , the probability of failure is:

$P_f=\int_\Omega I[g(\mathbf{x})\leq 0]\mathbf{f}_\mathbf{X}(\mathbf{x})\mathrm d\mathbf{x}$

An approximation of 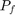$P_f$ is given by the Second Order Reliability Method (SORM) which assumes that the limit state function is quadratic in the standard normal space.

The SORM approximations available in this toolbox are:

'Breitung', Wu (1984)
'Tvedt', Tvedt (1990)
'Koyluoglu', Köylüoǧlu & Nielsen (1994)
'Cai', Cai & Elishakoff (1994)
'Zhao', Zhao & Ono (1999)
'Subset', uses Subset Simulations Au & Beck (2001) on a second order Taylor expansion

Parameters

param value Description

'Tinv' function_handle, { [ ] } An inverse transformation function that transform realizations from a standard gaussian space into the desired space. For example, for an exponential space Tinv=@(u)expinv(normcdf(u),1).

'approx' {'Breitung'}, 'Tvedt', 'Koyluoglu', 'Cai', 'Zhao', 'Subset' Defines which RIA solver to use, see Approximations.

'rel_diff' positive integer, {1e-5} Perturbation used for finite difference.

'res_form' structure, { [ ] } The result of a call to form. If empty, runs form with default.

'H' positive integer, { [ ] } Hessian matrix in the U space. If not provided, uses finite differences. Usefull after a first run, for recall.

'grad' positive integer, { [ ] } Gradient in the U space. If not provided, uses finite differences. Usefull after a first call run, for recall.

`param`	`value`	Description
'Tinv'	`function_handle`, { [ ] }	An inverse transformation function that transform realizations from a standard gaussian space into the desired space. For example, for an exponential space `Tinv=@(u)expinv(normcdf(u),1)`.
'approx'	{'Breitung'}, 'Tvedt', 'Koyluoglu', 'Cai', 'Zhao', 'Subset'	Defines which RIA solver to use, see Approximations.
'rel_diff'	positive integer, {1e-5}	Perturbation used for finite difference.
'res_form'	structure, { [ ] }	The result of a call to `form`. If empty, runs `form` with default.
'H'	positive integer, { [ ] }	Hessian matrix in the U space. If not provided, uses finite differences. Usefull after a first run, for recall.
'grad'	positive integer, { [ ] }	Gradient in the U space. If not provided, uses finite differences. Usefull after a first call run, for recall.

Example

Compute and plot a generalized "max-min" sample

g=@CODES.test.lin;
res=CODES.reliability.sorm(g,2);
disp(res)

          Pf: 0.0013
        beta: 3.0000
    LS_count: 15
         MPP: [2.1213 2.1213]
           H: [2x2 double]
           G: [-0.7071 -0.7071]

Mini Tutorial

A mini tutorial of the capabilities of the sorm function.

References

Breitung (1984): Breitung, K. (1984). Asymptotic approximations for multinormal integrals. Journal of Engineering Mechanics, 110(3), 357-366.
Tvedt (1990): Tvedt, L. (1990). Distribution of Quadratic Forms in Normal Space - Application to Structural Reliability. Journal of Engineering Mechanics, 116(6), 1183-1197. DOI
Köylüoǧlu & Nielsen (1994): Köylüoǧlu, H. U., & Nielsen, S. R. K. (1994). New approximations for SORM integrals. Structural Safety, 13(4), 235-246. DOI
Cai & Elishakoff (1994): Cai, G. Q., & Elishakoff, I. (1994). Refined second-order reliability analysis. Structural Safety, 14(4), 267-276. DOI
Zhao & Ono (1999): Zhao, Y.-G., & Ono, T. (1999). New Approximations for SORM: Part 1. Journal of Engineering Mechanics, 125(1), 79-85. DOI
Au & Beck (2001): Au, S.-K., & Beck, J. L. (2001). Estimation of small failure probabilities in high dimensions by subset simulation. Probabilistic Engineering Mechanics, 16(4), 263-277. DOI