edsd

Perform Explicit Design Space Decomposition

Syntax
Description
Plot functions
Parameters
Example
Mini Tutorial
References
See also

Syntax

Mcol=CODES.sampling.edsd(f,M,lb,ub) performs EDSD on f, using an initial meta-model M, within lb and ub and returns the collection of meta-model Mcol.
Mcol=CODES.sampling.edsd(...,param,value) uses a list of parameters param and values value (see parameter table).

Description

This function performs Explicit Design Space Decomposition (EDSD) as described in Basudhar and Missoum (2010) and Basudhar (2011). Essentially, EDSD sequentially refines an initial meta-model (an SVM in Basudhar's work) using max-min and anti-locking samples. Please refer to their specific documentation for details. This implementation relies on the numerical advances presented in Lacaze and Missoum (2014).

In Basudhar and Missoum (2008), a convergence metric is introduced based on the change of class of "convergence" samples from one iteration to another:

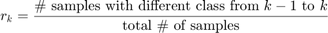
$r_k=\frac{\textrm{\# samples with different class from }k-1\textrm{ to }k}{\textrm{total \# of samples}}$

This ratio is further fitted by an exponential model:

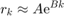
$r_k\approx A\mbox{e}^{Bk}$

where A and B (≤0) are constants to be determined and k the iteration considered. If 'conv_coef' is set to 'fit', A and B are chosen so as to minimize the least square error. If 'conv_coef' is set to 'direct' at iteration k, A and B are chosen such that:

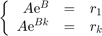
$\left\{\begin{array}{rcl}A\mbox{e}^B&=&r_1\\ A\mbox{e}^{Bk}&=&r_k\end{array}\right.$

The algorithm stops when both of the following conditions are satisfied:

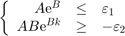
$\left\{\begin{array}{rcl}A\mbox{e}^B&\leq&\varepsilon_1\\ AB\mbox{e}^{Bk}&\geq&-\varepsilon_2\end{array}\right.$

where $\varepsilon_1$ and $\varepsilon_2$ are the user defined parameters:

'eps_1' and 'eps_2' respectively.

Plot functions

The edsd function can accept a 'plotfcn' option. A function or a cell array of functions can be passed to the method. These methods should be defined as:

function plotfcn(meta,iter)
    ...
end

where meta and iter are parameters passed to the function by edsd. iter is the last completed iteration and meta is the last trained meta (i.e., the one trained at the end of iteration iter). Each of these function is allocated a figure at the begining of edsd with:

hold on

For example:

function plot_meta(meta,iter)
    clf;
    meta.isoplot;
    title(['Iterations ' num2str(iter) ' completed'])
end

Parameters

param value Description

'schedule' (1 x 2) positive integer, { [2 1] } Schedule used to mix "max-min" and "anti-locking" samples. The default schedule, [2 1], specifies the use of 2 "max-min" iterations followed by 1 "anti-locking" iteration.

'iter_max' positive integer, {30} Number of iterations

'vectorized' logical, {true} Whether the function f is vectorized

'f_Parallel' logical, {false} If 'vectorized' is set to false, whether new samples should be evaluated in parallel

'extra_output' logical, {false} Whether the function f is returning a second output that needs to be stored and returned (this extra output should be a cell row array)

'conv' logical, {true} Should convergence be checked (true) or wait for max_iter (false) (see, Basudhar et al., 2008)

'plot_conv' logical, {false} Should convergence be plotted (requires 'conv' to be true)

'conv_coef' {'fit'} or 'direct' Method to compute coefficient of the exponential involved in the convergence

'eps_1' numeric, {4e-3} Tolerance on class change ratio

'eps_2' numeric, {5e-4} Tolerance on class change rate

'x_conv' numeric, {(1e4 x M.dim) LHS} Convergence points

'display_edsd' logical, {true} Display level

'plotfcn' cell or function_handle, { [ ] } A function or a cell array of functions to be executed at the end of each iteration, see Plot functions

`param`	`value`	Description
'schedule'	(1 x 2) positive integer, { [2 1] }	Schedule used to mix "max-min" and "anti-locking" samples. The default schedule, [2 1], specifies the use of 2 "max-min" iterations followed by 1 "anti-locking" iteration.
'iter_max'	positive integer, {30}	Number of iterations
'vectorized'	logical, {`true`}	Whether the function `f` is vectorized
'f_Parallel'	logical, {`false`}	If 'vectorized' is set to `false`, whether new samples should be evaluated in parallel
'extra_output'	logical, {`false`}	Whether the function `f` is returning a second output that needs to be stored and returned (this extra output should be a cell row array)
'conv'	logical, {`true`}	Should convergence be checked (`true`) or wait for max_iter (`false`) (see, Basudhar et al., 2008)
'plot_conv'	logical, {`false`}	Should convergence be plotted (requires 'conv' to be `true`)
'conv_coef'	{'fit'} or 'direct'	Method to compute coefficient of the exponential involved in the convergence
'eps_1'	numeric, {4e-3}	Tolerance on class change ratio
'eps_2'	numeric, {5e-4}	Tolerance on class change rate
'x_conv'	numeric, {(1e4 x `M.dim`) LHS}	Convergence points
'display_edsd'	logical, {`true`}	Display level
'plotfcn'	cell or `function_handle`, { [ ] }	A function or a cell array of functions to be executed at the end of each iteration, see Plot functions

In addition, options from anti_lock, mm and MultiStart can be used as well.

Example

Perform 5 iterations of EDSD and plot the SVM collection

DOE=CODES.sampling.cvt(20,2,'lb',[-5 -5],'ub',[5 5]);
svm=CODES.fit.svm(DOE,DOE(:,1)-DOE(:,2));
svm_col=CODES.sampling.edsd(@(x)(x(:,1)-x(:,2)),svm,[-5 -5],[5 5],'iter_max',5);
for i=1:5
    svm_col{i}.isoplot('new_fig',true,'lb',[-5 -5],'ub',[5 5])
    if i<5
        plot(svm_col{i+1}.X(end,1),svm_col{i+1}.X(end,2),'ms')
    end
end
axis square

EDSD: iteration 1 out of 5 is done
EDSD: iteration 2 out of 5 is done
EDSD: iteration 3 out of 5 is done
EDSD: iteration 4 out of 5 is done
EDSD: iteration 5 out of 5 is done
EDSD: Stopped because maximum number of iteration was reached

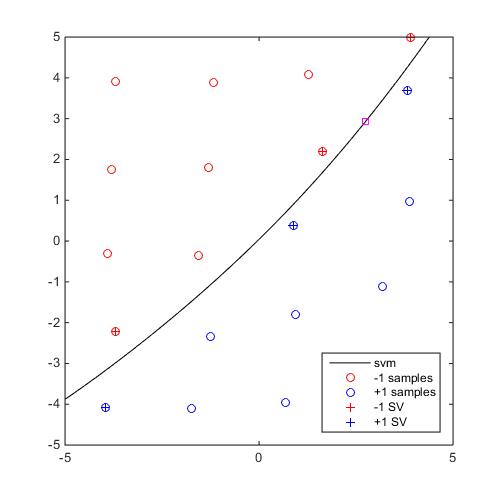
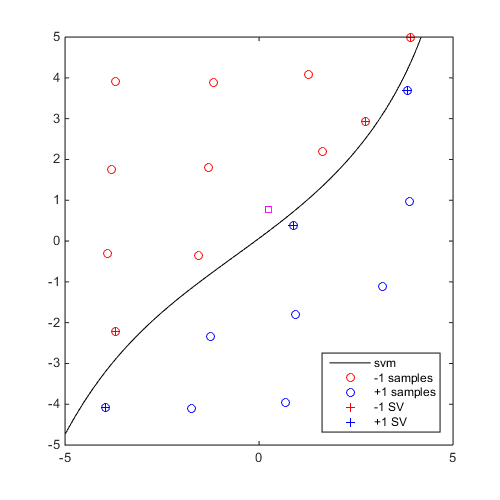
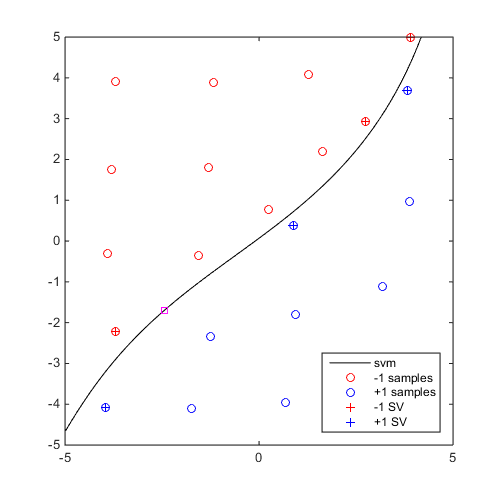
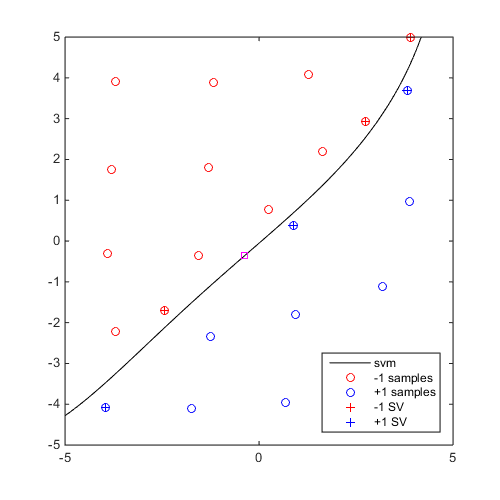
Mini Tutorial

A mini tutorial of the capabilities of the edsd function.

References

Basudhar and Missoum (2008): Basudhar A., Missoum S., (2008) Adaptive explicit decision functions for probabilistic design and optimization using support vector machines. Computers & Structures 86(19):1904-1917 - DOI
Basudhar and Missoum (2010): Basudhar A., Missoum S., (2010) An improved adaptive sampling scheme for the construction of explicit boundaries. Structural and Multidisciplinary Optimization 42(4):517-529 - DOI
Basudhar, 2011: Basudhar A., (2011) Computational optimal design and uncertainty quantification of complex systems using explicit decision boundaries. The University of Arizona - DOI
Lacaze and Missoum (2014): Lacaze S., Missoum S., (2014) A generalized "max-min" sample for surrogate update. Structural and Multidisciplinary Optimization 49(4):683-687 - DOI