anti_lock

Generates an anti-locking sample

Syntax
Description
Parameters
Example
Mini Tutorial
References
See also

Syntax

x_al=CODES.sampling.anti_lock(M,lb,ub) finds an anti-locking sample x_al on model M with lower bound lb and upper bound ub.
x_al=CODES.sampling.anti_lock(...,param,value) uses a list of parameters param and values values (c.f., parameter table).
[x_al,adds]=CODES.sampling.anti_lock(...) only if nb=1 and M.dim=2, returns a (1 x 2) cell,|adds|, made of center and points to plot region boundary (see, demonstration for more details).

Description

This function finds an anti-locking sample as introduced in Basudhar (2011). A first optimization problem searches a region of maximum unbalance as:

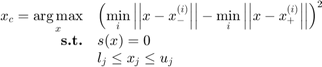
$\begin{array}{rl}x_c=\mathop{\arg\max}\limits_{x}&\left(\mathop{\min}\limits_{i}\left|\left|x-x_{-}^{(i)}\right|\right|-\mathop{\min}\limits_{i}\left|\left|x-x_{+}^{(i)}\right|\right|\right)^2\\\textbf{s.t.} & s(x)=0\\&l_j\leq x_j\leq u_j\end{array}$

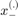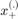where $x_{-}^{(.)}$ and $x_{+}^{(.)}$ are the negative and positive samples,respectively, used to train $s$ , a meta-model (an SVM in Basudhar's work). The numerical implementation of this optimization problem follows the steps highlighted in Lacaze and Missoum (2014) regarding the use of the Chebychev distance (infinite norm). This problem being made differentiable, it is then solve using multi-start SQP.

Once the center is found, a second optimization is carried out:

$\begin{array}{rl}x_{al}=\mathop{\arg\min}\limits_{x}&\mathop{\mathrm{sgn}}\biggl[\mathop{\min}\limits_{i}\left|\left|x_c-x_{-}^{(i)}\right|\right|-\mathop{\min}\limits_{i}\left|\left|x_c-x_{+}^{(i)}\right|\right|\biggr]s(x)\\\textbf{s.t.} & \left|\left|x-x_c\right|\right|-R\leq 0\\&l_j\leq x_j\leq u_j\end{array}$

where:

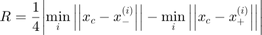
$R=\frac{1}{4}\biggl|\mathop{\min}\limits_{i}\left|\left|x_c-x_{-}^{(i)}\right|\right|-\mathop{\min}\limits_{i}\left|\left|x_c-x_{+}^{(i)}\right|\right|\biggr|$

Parameters

param value Description

'nb' positive integer, {1} Number of anti-locking samples requested (nb≥2 is refered to as parallel, unpublished)

'intensity' positive integer, {30} Number of starting points for the multi-start SQP algorithm

'UseParallel' logical, {M.UseParallel} Parallel set up usage

'MultiStart' {'CODES'}, 'MATLAB' Defines whether MATLAB or CODES multistart fmincon should be used.

'Display' {'off'}, 'iter', 'final' Defines the verbose level.

`param`	`value`	Description
'nb'	positive integer, {1}	Number of anti-locking samples requested (nb≥2 is refered to as parallel, unpublished)
'intensity'	positive integer, {30}	Number of starting points for the multi-start SQP algorithm
'UseParallel'	logical, {`M.UseParallel`}	Parallel set up usage
'MultiStart'	{'CODES'}, 'MATLAB'	Defines whether MATLAB or CODES multistart fmincon should be used.
'Display'	{'off'}, 'iter', 'final'	Defines the verbose level.

In addition, options from MultiStart can be used as well, when 'MultiStart' is set to 'MATLAB'.

Example

Compute and plot an anti-locking sample

DOE=CODES.sampling.cvt(20,2,'lb',[-5 -5],'ub',[5 5]);
svm=CODES.fit.svm(DOE,DOE(:,1)-DOE(:,2));
x_al=CODES.sampling.anti_lock(svm,[-5 -5],[5 5]);
figure('Position',[200 200 500 500])
svm.isoplot('lb',[-5 -5],'ub',[5 5])
plot(x_al(1),x_al(2),'ms')

Mini Tutorial

A mini tutorial of the capabilities of the anti_lock function.

References

Basudhar (2011): Basudhar A., (2011) Computational optimal design and uncertainty quantification of complex systems using explicit decision boundaries. The University of Arizona - DOI
Lacaze and Missoum (2014): Lacaze S., Missoum S., (2014) A generalized "max-min" sample for surrogate update. Structural and Multidisciplinary Optimization 49(4):683-687 - DOI