iform

Inverse first-order reliability method

Syntax
Description
Solvers
Parameters
Example
Demonstration
References
See also

Syntax

res=CODES.reliability.iform(g,dim,beta) search for the Minimum Performance Target Point (MPTP) at a given beta. The dimension dim of the problem must be specified.
res=CODES.reliability.iform(...,param,value) uses a list of parameters param and values value (see, parameter table)

Description

For a given target probability of failure associated with a target reliability index 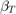$\beta_T$ , the inverse FORM approach finds the minimum performace target point (MPTP) 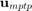$\mathbf{u}_{mptp}$ by solving the following optimization problem (PMA approach):

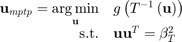
$\begin{array}{rl}\mathbf{u}_{mptp}=\mathop{\arg\min}\limits_{\mathbf{u}}&g\left(T^{-1}\left(\mathbf{u}\right)\right)\\\mbox{s.t.} & \mathbf{u}\mathbf{u}^T=\beta_T^2\end{array}$

For distribution hyper-parameters$\theta$ and deterministic variables $\mathbf{z}$ , the probabilistic performace measure (PPM) is defined as:

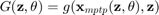
$G(\mathbf{z},\theta)=g(\mathbf{x}_{mptp}(\mathbf{z},\theta),\mathbf{z})$

Sensitivities of the PPM 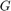$G$ are:

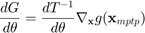
$\displaystyle\frac{dG}{d\theta}=\frac{dT^{-1}}{d\theta}\nabla_\mathbf{x}g(\mathbf{x}_{mptp})$

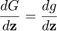
$\displaystyle\frac{dG}{d\mathbf{z}}=\frac{dg}{d\mathbf{z}}$

Solvers

Currently available solvers:

'sqp', matlab fmincon using sqp algorithm
'amv', Wu (1984)
'cmv', Youn et al. (2003)
'hmv', Youn et al. (2003)

Parameters

param value Description

'solver' {'sqp'}, 'amv', 'cmv', 'hmv' Defines which RIA solver to use, see Solvers.

'Tinv' function_handle, { [ ] } An inverse transformation function that transform realizations from a standard gaussian space into the desired space. For example, for an exponential space Tinv=@(u)expinv(normcdf(u),1).

'LS_grad' logical, {false} Wether the limit state function g also return gradients with respect to x.

'rel_diff' positive integer, {1e-5} Perturbation used for finite difference.

'eps' positive integer, {1e-4} Convergence tolerance.

'iter_max' positive integer, {100} Maximum number of iterations.

'vectorial' logical, {false} Wether the limit state function g is vectorial.

'display' {'none'}, 'final', 'iter' Defines the verbose level.

'gz' function_handle g as a function of x and z, used for dPPM/dz (see Mini Tutorial for an example).

'dgdz' function_handle dg/dz as a function of x and z, used for dPPM/dz (see Mini Tutorial for an example).

'z' real value z value, used for dPPM/dz (see Mini Tutorial for an example).

'T' function_handle Transformation T as a function of x and theta, used for dPPM/dtheta (see Mini Tutorial for an example).

'dTdx' function_handle dT/dx as a function of x and theta, used for dPPM/dtheta (see Mini Tutorial for an example).

'Tinvtheta' function_handle Inverse transformation Tinv as a function of u and theta, used for dPPM/dtheta (see Mini Tutorial for an example).

'dTinvdtheta' function_handle dTinv/dtheta as a function of u and theta, used for dPPM/dtheta (see Mini Tutorial for an example).

'theta' real value theta value, used for dPPM/dtheta (see Mini Tutorial for an example).

`param`	`value`	Description
'solver'	{'sqp'}, 'amv', 'cmv', 'hmv'	Defines which RIA solver to use, see Solvers.
'Tinv'	`function_handle`, { [ ] }	An inverse transformation function that transform realizations from a standard gaussian space into the desired space. For example, for an exponential space `Tinv=@(u)expinv(normcdf(u),1)`.
'LS_grad'	logical, {`false`}	Wether the limit state function `g` also return gradients with respect to x.
'rel_diff'	positive integer, {1e-5}	Perturbation used for finite difference.
'eps'	positive integer, {1e-4}	Convergence tolerance.
'iter_max'	positive integer, {100}	Maximum number of iterations.
'vectorial'	logical, {`false`}	Wether the limit state function `g` is vectorial.
'display'	{'none'}, 'final', 'iter'	Defines the verbose level.
'gz'	`function_handle`	g as a function of x and z, used for dPPM/dz (see Mini Tutorial for an example).
'dgdz'	`function_handle`	dg/dz as a function of x and z, used for dPPM/dz (see Mini Tutorial for an example).
'z'	real value	z value, used for dPPM/dz (see Mini Tutorial for an example).
'T'	`function_handle`	Transformation T as a function of x and theta, used for dPPM/dtheta (see Mini Tutorial for an example).
'dTdx'	`function_handle`	dT/dx as a function of x and theta, used for dPPM/dtheta (see Mini Tutorial for an example).
'Tinvtheta'	`function_handle`	Inverse transformation Tinv as a function of u and theta, used for dPPM/dtheta (see Mini Tutorial for an example).
'dTinvdtheta'	`function_handle`	dTinv/dtheta as a function of u and theta, used for dPPM/dtheta (see Mini Tutorial for an example).
'theta'	real value	theta value, used for dPPM/dtheta (see Mini Tutorial for an example).

Example

Compute and plot a generalized "max-min" sample

g=@CODES.test.lin;
res=CODES.reliability.iform(g,2,2.5);
disp(res)

          Pf: 0.0062
        beta: 2.5000
    LS_count: 20
        MPTP: [1.7678 1.7678]
       uMPTP: [1.7678 1.7678]
         PPM: 0.5000

Demonstration

A complete demonstration of the capabilities of the iform function.

References

Wu (1984): Wu, Y.-T. (1984). Efficient methods for mechanical and structural reliability analysis and design (safety-index, fatigue, failure). The University of Arizona. link
Youn et al. (2003): Youn, B. D., Choi, K. K., & Park, Y. H. (2003). Hybrid Analysis Method for Reliability-Based Design Optimization. Journal of Mechanical Design, 125(2), 221. DOI