CODES / reliability / subset
Subset Simulations
Contents
Syntax
- res=CODES.reliability.subset(g,dim) compute a Subset Simulation estimate of the probability that
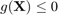 . The dim random variables
. The dim random variables 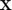 are independent standard gaussian.
are independent standard gaussian. - res=CODES.reliability.subset(...,param,value) uses a list of parameters param and values value (see, parameter table)
Description
For a given limit state function 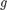 and a joint PDF
and a joint PDF 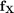 , the probability of failure is:
, the probability of failure is:
![$$P_f=\int_\Omega I[g(\mathbf{x})\leq
0]\mathbf{f}_\mathbf{X}(\mathbf{x})\mathrm d\mathbf{x}$$](subset_eq12939585862755613080.png)
A Subset Simulation (Au & Beck, 2001) estimates the probability of failure as a product of larger conditional probabilities:
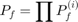
where 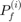 is the
is the 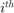 intermediate probability of failure. These intermediate probabilities are estimated by successive Markov-Chain Monte Carlo simulations (Au & Beck, 2001).
intermediate probability of failure. These intermediate probabilities are estimated by successive Markov-Chain Monte Carlo simulations (Au & Beck, 2001).
In general, the probability of failure is dependent on distribution hyper-parameters 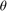 and deterministic variables
and deterministic variables  :
:
![$$P_f=\int I[g(\mathbf{x},\mathbf{z})\leq
0]\mathbf{f}_\mathbf{X}(\mathbf{x}|\theta)\mathrm d\mathbf{x}$$](subset_eq14312482567873613938.png)
Derivatives of the probability of failure can be derived for hyper-parameters:
![$$\begin{array}{rcl}\displaystyle\frac{dP_f}{d\theta}&=&\displaystyle\frac{d}{d\theta}\int I[g(\mathbf{x},\mathbf{z})\leq 0]f_\mathbf{X}(\mathbf{x}|\theta)d\mathbf{x}\\&=&\displaystyle\int I[g(\mathbf{x},\mathbf{z})\leq 0]\frac{d\ln f_\mathbf{X}}{d\theta}f_\mathbf{X}(\mathbf{x}|\theta)d\mathbf{x}\end{array}$$](subset_eq03224261944129265684.png)
An expression of sensitivity estimates with respect to 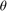 as a cross-product of the Subset Simulation can be found in Song et al. (2009).
as a cross-product of the Subset Simulation can be found in Song et al. (2009).
![$$\begin{array}{rcl}\displaystyle\frac{dP_f}{d\mathbf{z}}&=&\displaystyle\frac{d}{d\mathbf{z}}\int I[g(\mathbf{x},\mathbf{z})\leq 0]f_\mathbf{X}(\mathbf{x}|\theta)d\mathbf{x}\\&=&\displaystyle-\int\frac{dg}{d\mathbf{z}}\delta[g(\mathbf{x},\mathbf{z})]f_\mathbf{X}(\mathbf{x}|\theta)d\mathbf{x}\end{array}$$](subset_eq08537904488808170917.png)
An expression of sensitivity estimates with respect to  as a cross-product of the Subset Simulation can be found in Lacaze et al. (2015).
as a cross-product of the Subset Simulation can be found in Lacaze et al. (2015).
Parameters
| param | value | Description |
|---|---|---|
| 'PDFs_target' | function_handle, { [ ] } | Target marginal pdfs. For a (n x dim) sample, PDFs_target(x) should return a (n x dim) matrix of marginal PDF values. Default is @(x)normpdf(x). |
| 'sampler' | function_handle, { [ ] } | A function to get samples for the first step. Default is @(N)normrnd(0,1,N,dim). |
| 'prop_rand' | function_handle, { [ ] } | Proposal random sampler. For a (n x dim) sample x, returns a (n x dim) sample of proposed candidates. By default, uses normal with mean x and standard deviation 1. |
| 'CoV' | numeric, {1} | Coefficient in % to be achieved on the CMC estimate of the first intermediate probability. |
| 'N' | numeric, { [ ] } | Number of samples to be used at the first step. If default, uses 'N' such that 'CoV' is satisfied. |
| 'CoV_bound' | logical, {false} | Wether the bound of the estimator coefficient of variation should be computed. Note that it might substantially increase the computational time. |
| 'step_Pf' | numeric, {0.1} | Step probability of failure. |
| 'verbose' | logical, {false} | Verbose level. |
| 'burnin' | positive integer, {0} | Number of samples to be “burned” at the begining. |
| 'store' | logical, {false} | Wether the Monte-Carlo sample should be stored and returned. |
| 'Pf_limit' | positive integer, {1e-8} | Lowest probability to be estimated. |
| 'vectorial' | logical, {false} | Wether the limit state function g is vectorial or not. Vectorization should always be used if possible and 'vectorial' set to true. |
| 'lnPDF' | function_handle | Log of joint PDF as a function of (x,theta) for dPfdtheta (see Mini Tutorial for an example). |
| 'dlnPDF' | function_handle | Derivative of log of joint PDF with respect to theta as a function of (x,theta)for dPfdtheta (see Mini Tutorial for an example). |
| 'theta' | real value | Theta value for dPfdtheta (see Mini Tutorial for an example). |
| 'nz' | positive integer | Number of deterministic variables for dPfdz. g is expected to return two outputs, g values and g gradients with respect to z (see Mini Tutorial for an example). |
| 'frac' | positive integer | Alpha fraction for dPfdz (see Mini Tutorial for an example and Lacaze et al. for details). |
| 'dirac' | {'gauss'}, 'tgauss', 'poisson', 'sinc', 'bump' | Dirac approximation function (see Mini Tutorial for an example and Lacaze et al. for details). |
Example
Compute and plot a generalized "max-min" sample
g=@CODES.test.lin;
res=CODES.reliability.subset(g,2,'vectorial',true);
disp(res)
Pf: 0.0013
beta: 3.0060
steps: 3
LS_count: 269275
Demonstration
 |
A complete demonstration of the capabilities of the subset function. |
References
- Au & Beck (2001): Au, S.-K., & Beck, J. L. (2001). Estimation of small failure probabilities in high dimensions by subset simulation. Probabilistic Engineering Mechanics, 16(4), 263-277. DOI
- Song et al. (2009): Song, S., Lu, Z., & Qiao, H. (2009). Subset simulation for structural reliability sensitivity analysis. Reliability Engineering & System Safety, 94(2), 658-665. DOI
- Lacaze et al. (2015): Lacaze, S., Brevault, L., Missoum, S., Balesdent, M. (2015). Probability of failure sensitivity with respect to decision variables. Structural and Multidisciplinary Optimization, First Published Online. DOI
See also
Copyright © 2015 Computational Optimal Design of Engineering Systems (CODES) Laboratory. University of Arizona.

|
Computational Optimal Design of Engineering Systems |

|